アニメーションです。
https://kats.issp.u-tokyo.ac.jp/kats/craftsman/index.html
位相速度は伝送線路を伝搬する 単一正弦波の等位相面の伝搬速度、 群速度 は周波数が僅かに異なる２つの正弦波の合成波形からできる 包絡線の伝搬速度で、 伝送線路の２次定数で表現すると、それぞれ下記のようになります。
http://www.mogami.com/puzzle/pzl-24.html
Contents
ドブロイ波の並みの速さは群速度です
https://www.mns.kyutech.ac.jp/~okamoto/education/physicsIIB/debroglie-groupvelocity-qa060208.pdf
重ね合わせではなく、変調。
https://eman-physics.net/math/group_vel.html
https://home.hiroshima-u.ac.jp/ino/lecture/SSP1note9_ino2017.pdf
https://home.hiroshima-u.ac.jp/kyam/pages/results/monograph/Ref03_deBroglie.pdf
電子の波長？？？
http://www.c.s.osakafu-u.ac.jp/~matuzaka/cluster/class/inorg.chem1/ic1supple1-05.pdf
波動関数に虚数単位がある意味。
なんかいろいろやっている
https://home.hiroshima-u.ac.jp/kyam/pages/results/monograph/Ref03_deBroglie.pdf
これは重要だー！！！！
https://home.hiroshima-u.ac.jp/kyam/pages/results/monograph/Ref03_deBroglie.pdf
質量があるもの（物＝粒子）を、質量のないもの（事＝波）として扱う異常さ。
https://www.osaka-med.ac.jp/deps/che/hayashi/Quantum_mechanics_history03.html
https://www1.doshisha.ac.jp/~bukka/lecture/quantum/pc3/pc3_02.html
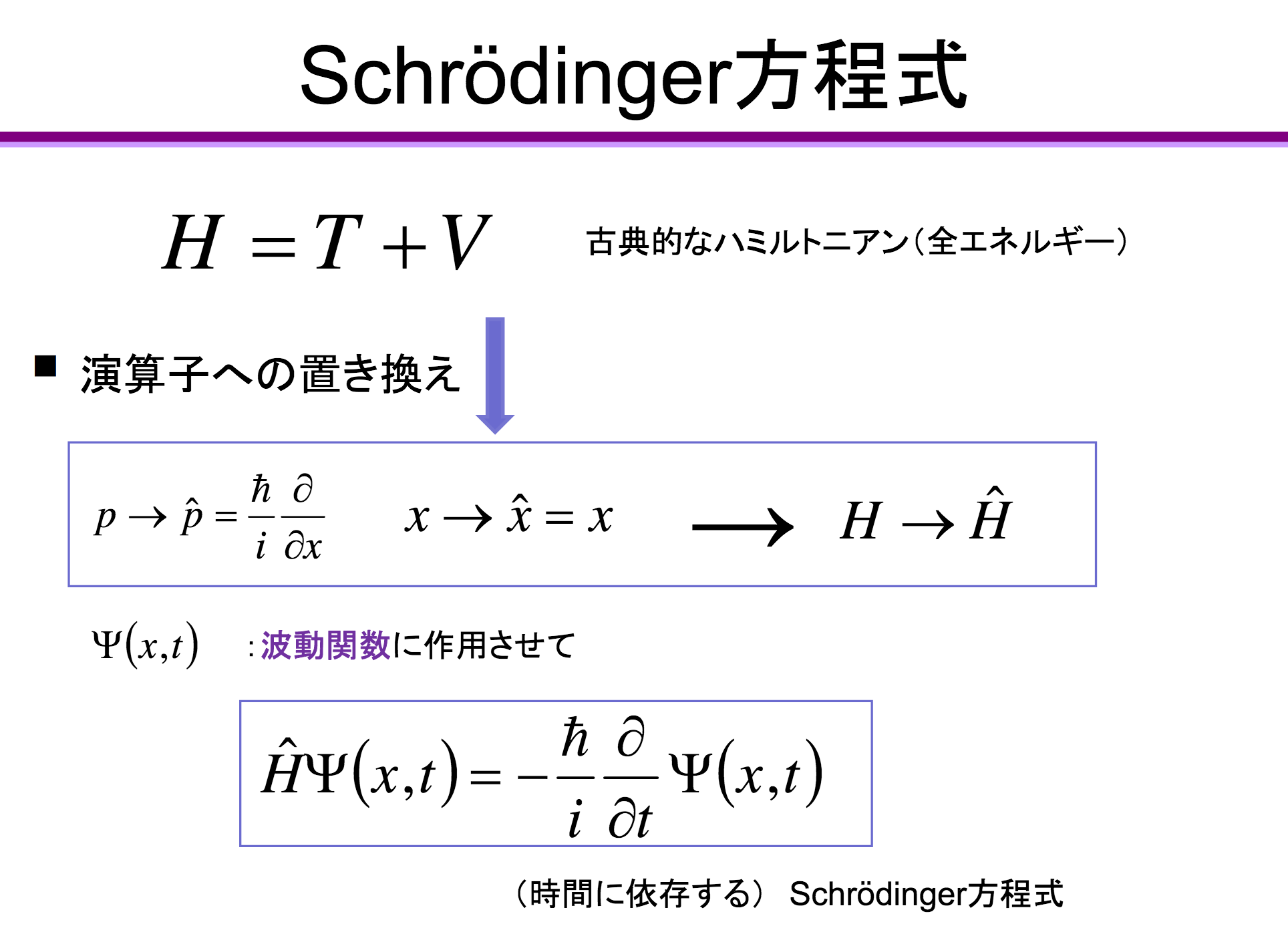
シュレーディンガー 
(オーストリア: 1887 – 1961) は ド・ブローイの物質波 (ド・ブローイ波) の アイデアに興味を持ち， この波動がどのような 方程式で 記述されるのか 検討した結果， １つの波動方程式を得ました (1926)． これが シュレーディンガーの 波動方程式 です． 通常は単に シュレーディンガー方程式 と呼ばれています．
http://ne.phys.kyushu-u.ac.jp/seminar/MicroWorld2/2Part1/2P13/Schroedinger_eq.htm
| 古典論では ニュートンの運動方程式 によって 粒子の軌道や運動量を， すべての時間にわたって 決定することが できました． ところが 量子力学の 基本方程式である シュレーディンガー 方程式が決定するのは 波動関数 です． そして波動関数から わかるのは 粒子の “存在確率” です． 何だか物足りないような 感じがしますが， ミクロの世界を 記述するには これで必要かつ十分 なのです． 前ページで学んだ ハイゼンベルクの 不確定性原理 に 照らし合わせて， ぴったり整合してるのです． このことは，このセミナー を通じて，だんだんと 分かってくるだろうと 思います． |
ne.phys.kyushu-u.ac.jp/seminar/MicroWorld2/2Part1/2P15/wavefunction.htm
「位相速度」「群速度」
https://eman-physics.net/math/group_vel.html
https://ocw.kyoto-u.ac.jp/ja/09-faculty-of-engineering-jp/quantum-theory-for-electrical-and-electronic-engineering/pdf/chap11.pdf
https://ocw.kyoto-u.ac.jp/ja/general-education-jp/4322001/video0727
量子力学では群速度の方が重要だということはわかったのですが、位相速度の方が重要な場合っ てどんなものがあるんでしょう？？
うーん、基本的には群速度の方が大事です。エネルギーやら運動量やらの伝 達速度も群速度の方で決まります。http://www.phys.u-ryukyu.ac.jp/~maeno/qm2006/qmK_2.html
http://irobutsu.a.la9.jp/movingtext/Vgvp/index.html#page1
これ詳しい！
http://www2.kobe-u.ac.jp/~lerl2/QPE(I)_05_01_08.pdf
